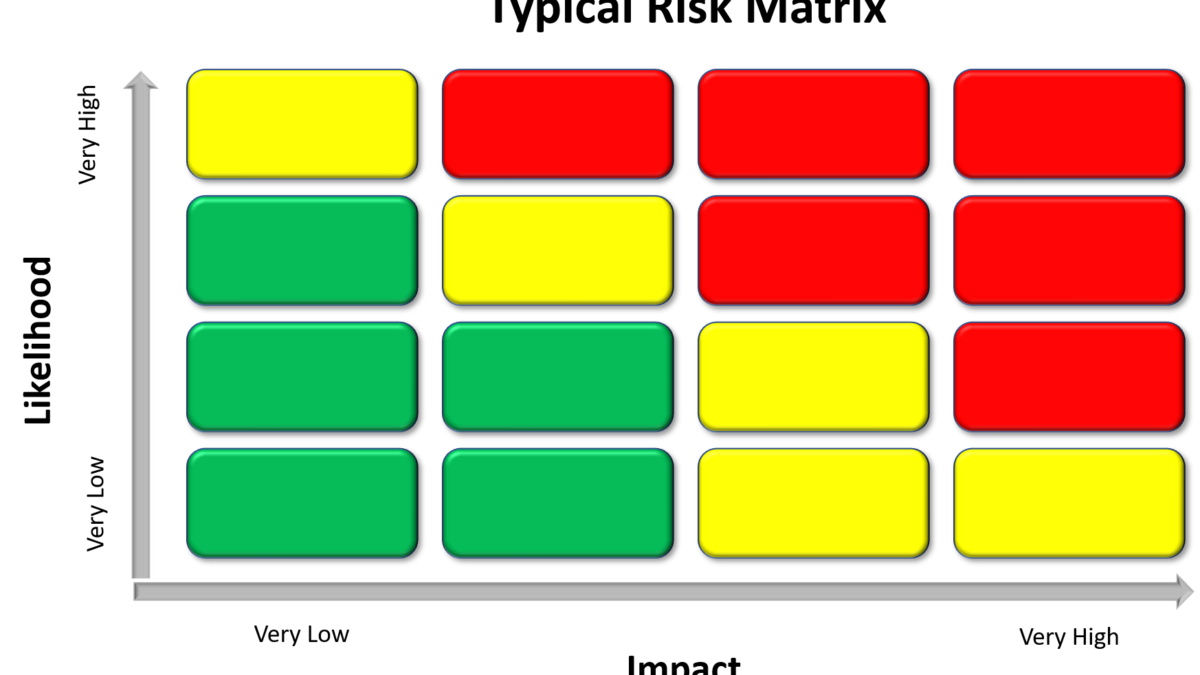
Most readers will be familiar with the above linear Risk Matrix Model. This graphical representation of risk exposure is useful but strict adherence to it can lead to a false sense of security.
Systemic Risk Management
The real world is very complex with many moving parts. The potential interaction of processes, events and other challenges can lead to disaster. It is often the case that the combination of a number of seemingly unrelated and in and of themselves potentially minor events can lead to catastrophe.
A systemic approach to risk exposure is appropriate. Field operations usually involves several to many somewhat disparate processes and individuals.
Typically, the operator will have individuals in the field as well as the office working together. Contractors and sub-contractors are similarly constructed. The number of interactions can grow exponentially in a large project or program.
Therefore, it is important to ‘see’ risk as a dynamic interacting model. For example, the following quotation is a straightforward presentation of the actual risk field operators face.
“Planning for the abandonment of Macondo was extremely complex. The fundamental source of that complexity was a phenomenon well known to systems engineers: the number of potential pairwise interactions among a set of N elements grows as N times N-1, divided by 2. That means that if there are two elements in the set, there is one potential interaction; if there are five elements, there are ten potential interactions; ten elements and there are forty-five; and so forth. If the interactions are more complex, such as when more that two things combine, the number is larger. Every potential interaction does not usually become an actual one, but adding the elements to a set means that complexity grows much more rapidly than ordinary intuition would expect.”
The authors’ note that NOT all combinations can happen, but the possibility of several is likely. Many decision makers do not expect exposures as great as they likely are in a complex environment.
Interactive Model
So how great is your risk? The following calculator will give you a perspective on your organization’s exposure. It is straightforward and easy to use.
You are only required to input two variables:
n = the number of elements
m = elements from n in certain order, it is arrangement
Taken from the Macondo model above, if n=10 and m=2, the number of combinations of m from n equals 45.
Addition data the calculator provides:
Each ordered set of n is a permutation
Generally, the number of combinations of m from n with repetitions is not useful for our purposes other than the recognition that repetition is possible.
This calculator does not indicate where risk lies. As the authors of Deepwater Horizon: A Systems Analysis of the Macondo Disaster suggest, it helps decision makers better understand the nature of their complex environment.
Final Thoughts
Simple risk models may have their place. They are useful for presentation purposes. However, they are insufficient when assessing the exposure of today’s complex operational situations.
High Reliability Management requires that decision makers NOT simplify the complex. Understanding the level of exposure using systemic risk management techniques can help clarify organizational threats.
Are Your Organization’s Risk Management Techniques Robust Enough?
For more information on Risk Mitigation check out our Operational Excellence Platform.
Boebert, Earl and Blossom, James M. (2016). Deepwater Horizon: A Systems Analysis of the Macondo Disaster. Cambridge, MA: Harvard University Press. pp. 65-66.
Appendix–The Math
For those interested, this is the math for the calculator. It is taken directly from the Planetcalc website.
So, assume we have a set of n elements.
Each ordered set of n is called permutation.
For example, we have set of three elements – А, В, and С.
Example of ordered set (one permutation) is СВА.
Number of permutations from n is
Example: For set of А, В, С number of permutations is 3! = 6. Permutations: АВС, АСВ, ВАС, ВСА, САВ, СВА
If we choose m elements from n in certain order, it is arrangement.
For example, arrangement of 2 from 3 is АВ, and ВА is the other arrangement. Number of arrangements of m from n is
Example: For set of А, В, С number of arrangements of 2 from 3 is 3!/1! = 6.
Arrangements: АВ, ВА, АС, СА, ВС, СВ
If we choose m elements from n without any order, it is combination.
For example combination of 2 from 3 is АВ. Number of combinations of m from n is
Example: For set of А, В, С number of combinations of 2 from 3 is 3!/(2!*1!) = 3.
Combinations: АВ, АС, СВ
Here is the dependency between permutations, combinations and arrangements